4 osztályos    

matematika

magyar szlovák

 

    
8 osztályos    

matematika

magyar

szlovák

 

  1. Végezd el!
    84 - 44 : 4 + 7 . 8 =
    130 - ( 15 - 3 5 ) . 103 =
    1564 : 4 + 139 27 =

    105 - 42 : 3 + 6 . 4 =
    105 - ( 42 : 3 + 6 ) . 4 =
    ( 105 - 42 ) : ( 3 + 6 ) . 4 =
  2. Melyik az a szám, amely
    a) 2314-nél 319-cel kisebb
    b) 3200 felénél 395-tel nagyobb
    c) 95-tel kisebb, mint 190-nek a 11-szerese?
  3. Határozd meg, melyik szám lesz a 823, 821, 819, ... számsorban az
    a) 5-ik
    b) 50-ik!
  4. Sorold fel az összes olyan háromjegyü számot melyröl tudjuk, hogy számjegyeinek szorzata 6!
  5. Tréfi kiradírozott néhány számjegyet Okoska matekfüzetéböl. Segíts Okoskának, írd be a csillagok helyére a hiányzó számjegyeket!

    3 * 5 *
          x 4
    ----------
    * 8 * 2
  6. Gombóc Artúr a mérleg egyik serpenyöjébe egy egész és egy harmad, a másikba egy fél tábla mogyorós csokoládét tett. Egy tábla csokoládé 300 gramm. Hány grammos súlyt tegyen a másik serpenyöbe, hogy a mérleg egyensúlyban legyen?
  7. A piacon 3 almát és két krumplit 1 káposztára lehet cserélni. Ugyanakkor 4 almáért 2 krumplit lehet kapni.
    a) Hány almáéert lehet kapni 1 káposztát?
    b) Hány krupliért adnak 1 káposztát?
  8. Két béka egyszerre indul a tó felé. A kis béka 6 cm-es, a nagy béka 10 cm-es ugrással halad. Hány ugrás után lesz a nagy béka 60 cm-rel a kis béka elött, ha a két béka mindig egyszerre ugrik?
  9. Zsebibaba és Kanga meglátogatja Micimackót. Zsebibaba feleakkorát ugrik mint Kanga. Kanga Micimackó házáig 38-at ugrik.
    a) Mennyit ugrik Zsebibaba?
    b) Milyen messze van Micimackó háza, ha Zsebibaba minden ugrása 50 cm?
  10. Karácsonykor nagy ünnepség volt Micimackónál. Eljött mind a 8 barátja. Mindenki kedveskedett valamilyen ajándékkal mindenkinek. Hány csomag került a fa alá?
  11. Kati a nyári szünidöben a nagymamánál nyaralt. Üdülése során 7-szer esett az esö délelött vagy délután. Olyan nem volt hogy egész nap esett volna az esö. Összesen 5 esötlen délelött és 6 esötlen délután volt. Hány napig nyaralt Kati a nagymamánál?

  12. Az ábrán egy kerítéssel bekerített kert látható. A kerten kívül, annak két sarkánál két fiú áll. Az A pontban álló András a B pontban álló Balázsra várakozik. Melyik útvonalon haladjon Balázs, hogy Andrásnak ne kelljen rá sokáig várni? Rajzold be! Balázs a kerten kívül bármerre mehet, nincs más akadály az útjában.

 

  1. Számítsd ki: (1010 -202) : 8
  2. (2754 - 753) : (71 - 88)
  3. A raktárban 190 kg burgonya és 110 kg-mal kevesebb vöröshagyma volt. Fokhagyma 4-szer kevesebb volt, mint vöröshagyma. Hány kg foghagyma volt a raktárban?
  4. Ferencnek ugyanannyi lánytestvére van mint fiútestvére. A lánytestvéreinek kétszer kevesebb lánytestvére van mint fiútestvére. Hány lány és hány fiú van a családban?
  5. A 100 oldalas könyv minden oldala meg van számozva. Hányszor fordul elő az egyes számjegy?
  6. A dominókat bizonyos szabály szerint raktuk sorba. Határozzátok meg a szabályt! Hány pontot kell rajzolni a kérdőjel helyére?

    wpe3.jpg (7323 bytes)
  7. Az 58293710822743 számok közül törölj ki 5 számjegyet úgy, hogy:
    a) a lehető legnagyobb
    b) a lehető legkisebb számot kapd!
  8. Hány háromszöget és hány négyzetet látsz az ábrán?

    wpeF.jpg (3029 bytes)

 

  1. Számítsátok ki   (240 - 16) : 8 =
                             2. 378 - 16 : 2 =
  2. Ebből a 9 számkártyából egyszerre 3 darab háromjegyű számot készíthetsz.

    wpe5.jpg (3555 bytes)

    Készítsd el úgy a 3 háromjegyű számot, hogy
    a)  a 3 szám összege a lehető legkisebb legyen. Mekkora ez az összeg?
    b)  a 2 nagyobb szám különbsége egyenlő legyen a legkisebb háromjegyű számmal.
    c) Számítsd ki a lehetséges legnagyobb és legkisebb háromjegyű szám különbségét!
  3. Az automata 1-es és 2-es gombját nyomtam meg: sonkát és zsemlét adott. Megnyomtam az 1-es, 3-as és 4-es gombot: narancsot, süteményt és zsemlét adott. Amikor a 4-es és 5-ös gombot nyomtam meg, akkor süteményt és fagylaltot kaptam. Mit adna a gép, ha a 3-as és 5-ös gombját nyomnám meg?
  4. Hány olyan háromjegyű szám van (100, 101,..., 999), amelyekre érvényes, hogy az első és a második számjegy összege éppen a harmadik számjegy.
  5. Egy csiga 15 méter mély kútba esett. Nappal 5 métert mászik felfelé, éjjel 4 métert csúszik vissza. Hányadik napon szabadul ki?
  6. Édesanya rétest készít. Kilenc lapot nyújt ki, miközben a szélét körben leszedi. Hány újabb réteslapot nyújthat a maradékból, ha három maradékból lesz egy újabb réteslap?
  7. Oszd fel az óra számlapját két egyenessel 3 olyan részre, hogy az egyes részekben lévő számok összege egyenlő legyen!

  8. wpe6.jpg (2823 bytes)

    a) végy el az első ábrából 3 gyufaszálat úgy, hogy három négyzet maradjon!
    b) végy el a második ábrából 2 gyufaszálat úgy, hogy két négyzet maradjon!
  9. Négy testvér egy telket vásárolt, melyen négy kút volt. Hogyan osztották fel egymás között, hogy mindenkinek jusson egy-egy kút, egy-egy ugyanolyan nagyságú és alakú egybefüggő föld?

    wpe7.jpg (6349 bytes)
  10. Szende, Szundi, Morgó, Tudor, Vidor, Hapci és Kuka a jövő hét minden napjára zsúrt tervez. Mindegyik zsúron 3 törpe venne részt, és mindenki mindenkivel pontosan egyszer akar találkozni. Hogyan szervezzék?

 

  1. Számítsd ki: (60-20).3 = (4+11).2+3 =
                           60-20.3 = 4+11.2+3 =
  2. Adott a következő négy "egyenlőség" :

    1   2   3 = 1
    1   2   3   4 = 1
    1   2   3   4   5 = 1
    1   2   3   4   5   6 = 1

    A számjegyek sorrendjének megváltoztatása nélkul tegyetek közéjük + - : . aritmetikai jeleket és zárójeleket úgy, hogy fennálljanak az egyenlőségek!
  3. Tedd igazzá az adott egyenlőtlenségeket! Keresd meg a négyzetbe írható legkisebb és legnagyobb egész számot!

    wpe8.jpg (1621 bytes)
  4. Amikor Kati, Mari és Zsuzsi találkoztak, nevetve állapították meg, hogy blúzuk formája teljesen egyforma, csak mindenki‚ más színű: piros, kék, zöld. Melyiküknek milyen színü a blúza, ha:
    Kati blúza nem kék
    Mari blúzának színe vagy zöld, vagy kék
    Zsuzsi blúza se nem piros, se nem zöld
  5. Folytasd! 2, 5, 7, 12, 19, 31, (írj még négy számot!)
  6. Melyek azok a kétjegyű számok, melyek számjegyeinek összege 7 ?
  7. Hány olyan háromszöget tudsz rajzolni, amelynek csúcsai a kijelölt pontok?
                 . A

    B .                   . C

                . D
  8. Egy fa törzsén felfelé mászik egy csiga. Nappal 4 métert mászik fel, éjjel azonban 3 métert csúszik vissza. A 9. napon este felér a fa csúcsára. Milyen magas a fa?
  9. Egy 3 x 3 x 3-as kockát kék színűre festünk, majd 1 x 1 x 1-es kockákra daraboljuk fel. Hány olyan kis 1 x 1 x 1 -es kocka lesz, melynek
    6 oldala kék,
    5 oldala kék
    4 oldala kék
    3 oldala kék
    2 oldala kék
    1 oldala kék
    egy oldala sem kék
  10. Négyzethálós papíron kerítsünk körül különbözőképpen öt egybevágó négyzetet úgy, hogy mindengyiknek legyen legalább egy közös oldala egy másikkal, vagyis a kis négyzetek egyetlen összefüggő síkidomot alkossanak. Hány különböző síkidomot tudunk így papírra rajzolni, ha kikötjük, hogy nem számít különbözönek két alakzat, ha kivágva az egyik a másikkal valamiképpen lefedhető.
 
  1. Végezd el: 64 - 20 : 4 - 6 . 5 =
    6 . 9 + 42 : 6 - 57 =
    ( 70 : 7 ) . 2 + 20 : 4 =
    (7600 + 34 . 100 ) : 10 =
  2. a) Számítsd ki: 4 . 12 + 18 : 2 =
    b) Helyezz el zárójeleket úgy, hogy más és más eredményt kapj. Írd fel az összes lehetőséget és számítsd is ki!
    4 . 12 + 18 : 2 =
    4 . 12 + 18 : 2 =
    4 . 12 + 18 : 2 =
  3. Folytasd a megkezdett számsort! Írd le a követekező két tagot!
    1, 1, 2, 3, 5, 8, 13, .....
    1, 2, 6, 24, 120, .....
    17, 15, 20, 18, 23, 31, ....
  4. Számítsd ki a 2, 5, 8 számjegyekből előállítható legnagyobb és leghisebb háromjegyű szám különbségét! (Egy számon belül a számjegyek nem ismétlődhetnek!)
  5. Rajzolj három egyenest úgy, hogy
    a) ne legyen metszéspontjuk
    b) 1 metszéspontjuk legyen
    c) 2 metszéspontjuk legyen
    d) 3 metszéspontjuk legyen
  6. Vágd el különbözőképpen mind a három négyzetet négy egyforma alakú és méretű részre, hogy mindegyik részben 3 darab csillag legyen!

  7. wpe10.jpg (5678 bytes)

    a) Hány 1 cm élű kis kockából tudod megépíteni az ábrán látható lépcsőt?
    b) Határozd meg a szükséges kockák számát, ha a lépcső magassága 7, 8, 9, 10!
    Válaszaidat indokold meg!
  8. Ügyi és Okoska azon tanakodik, hogy 2 cm, 4 cm és 6 cm-es pálcikákból hány különböző háromszöget lehet kirakni, ha mindegyik méretből 3 pálcikájuk van és minden háromszög kirakásához 3 pálcikát használhatnak fel.

 

  1. Végezd el:
    42 - 30 : 6 + 1 =
    103 - (12 - 2 . 6) . 20 =
    (8100 + 19 . 100) : 10 =
    327 . 13 - 1715 : 7 =
  2. Írd be a megfelelő számokat a keretekbe!
    wpe44.jpg (3218 bytes)
  3. Töltsd ki a táblázatot úgy, hogy bármely 3 egy sorban vagy egy oszlopban lévő, egymással szomszédos négyzetbe írt szám összege 6 legyen. (Két négyzet szomszédos, ha van közös oldaluk.)

    wpe1D.jpg (3716 bytes)
  4. Sorold fel az összes kétjegyü számot, melyre igaz, hogy számjegyeinek szorzata 6!
  5. Leírtuk az összes 1997-nél kisebb természetes számot, majd áthúztuk azokat, amelyekben 1 darab 1-es, 2 darab 9-es és 1 darab 6-os számjegy szerepel.
    a) Sorold fel, melyeket húztuk át!
    b) Hány számot nem húztunk át?
  6. Egy öttagú család életkorának összege 75 év.
    a) Hány év volt életkoruk összege két évvel ezelőtt?
    b) Hány év múlva lesz életkoruk összege 100 év?
    Írd le, hogy számoltál!
  7. Palacsintás király 77 palacsintát rendelt szakácsától vacsorára. A szakács 1 perc alatt egyszerre 5 palacsintát tud kisütni. Amikor azonban a következő adag kisütéséhez kezd, mindig eltűnik a kisütött palacsintákból 4 darab. Ilyen körülmények között legkevesebb hány perc múlva tud feltálalni 77 palacsintát?
    Válaszodat indokold meg!
  8. Hány 6 cm és 4 cm oldalú téglalapra lehet feldarabolni egy 60 cm oldalú négyzetet?
  9. Szerkesszétek meg a PQR háromszöget, ha |PQ| = 58 mm, |QR| = 34 mm, |RP| = 68 mm!
  10. Egy kockát 3 helyzetben rajzoltunk le. Írd az ábra alá a kocka alján lévő pontok számát! (Elnézést kérünk, de a feladathoz tartozó ábra nem áll rendelkezésünkre )

 

  1. Végezd el!
    105 - 42 : 3 + 6 . 4 = 114
    105 - (42 : 3 + 6 ) . 4 = 25
    ( 105 - 42 ) : (3 + 6 ) . 4 = 28
  2. Melyik az a szám,amely
    a) 2314-nál 319-cel kisebb?
    b) 3200 felénél 395-tel nagyobb?
    c) 95-tel kisebb, mint 190-nek a 11-szerese?
  3. Sorold fel az összes olyan háromjegyű számot melyről tudjuk, hogy számjegyeinek a szorzata 6!
  4. Gombóc Artúr a mérleg egyik serpenyőjébe egy egész és egy harmad, a másikba egy fél tábla mogyorócsokoládét tett. Egy tábla csokolád‚ 300 gramm. Hány gramos súlyt tegyen a másik serpenyőbe, hogy a mérleg egyensúlyban legyen?
  5. Két béka egyszerre indul a tó felé. A kis béka 6 cm-es, a nagy béka 10 cm-es ugrással halad.Hány ugrás után lesz a nagy béka 60 cm-rel a kis béka előtt, ha a két béka mindig egyszerre ugrik?
  6. Kati a nyári szünidőben a nagymamánál nyaralt. Üdülése során 7-szer esett az eső délelőtt vagy délután.Olyan nem volt, hogy egész nap esett volna az eső. Összesen 5 esőtlen délelőtt és 6 esőtlen délután volt.Hány napig nyaralt Kati a nagymamánál?
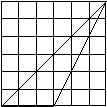
  7. Hány útvonalon juthatsz el az A pontból a B pontba, ha csak jobbra és felfelé mehetsz?

  8. A rajz egy telek alaprajza, amelyen négy kút van.Hogyan lehet a telket négy ugyanakkora és ugyanolyan alakú részre felosztani, hogy mindegyiken 1-1 kút legyen?


  9. Az alábbi testhálók közül melyikből lehet kockát hajtogatni? Írd az ábrák alá IGEN - NEM!

    primoMat97_9.gif (1943 bytes)
  10. Egy négyzet oldala 4 cm. Darabold fel a négyzetet
    a) 4
    b) 7
    c) 8 darab négyzetre!

 

  1. Végezd el:
    131 – 68:4 + 3.6 =
    131 – (68:4 + 3) . 6 =
    (131 – 68) : (4 + 3) . 6 =
  2. Melyik az a szám, amely
    a) 1234-nél 567-tel kisebb
    b) 1100 felénél 117-tel nagyobb
    c) 84-gyel nagyobb, mint 174-nek a 11-szerese?
  3. Radírpók leradírozott Picúr házi feladatából néhány számjegyet. Segíts Picúrnak, írd be a hiányzó számjegyeket!
    2 ... 5 ...
            x 3          ( x - szorozva)
    –––––––
    ... 9 ... 2
  4. Egy iskola tanulói vonattal szeretnének utazni. A vonat 14 kocsiból áll. A 4. osztályos tanulóknak elölről számolva a 4. kocsiba kell beszállni. Az állomáson a vonat végéhez érnek. Hátulról számolva hányadik kocsiba kell beszállniuk?
  5. Barbapapa és Barbamama egymással sakkoztak. Barbapapa 5 alkalommal nyert és 2 alkalommal döntetlent játszott. Barbamama 4 alkalommal nyert és 5 mérkőzést elveszített. Hány mérkőzést játszottak?
  6. Frakk 10 másodperc alatt 100 métert tesz meg, Lukrécia pedig 80 métert. Mennyi idő múlva éri utol Frakk Lukréciát, ha Lukréciának 180 méter előnye van?
  7. A háromszög oldalainak hossza 6 cm, 7 cm és 11 cm. Mekkora annak a négyzetnek az oldala, amelynek ugyanakkora a kerülete mint a háromszögnek?
  8. Hány különböző háromszöget látsz az ábrán?


  9. Egy kocka éleinek mindegyikét vagy pirosra vagy zöldre festettük. A kocka mindegyik lapján van legalább egy piros él. Legkevesebb hány élét festettük pirosra?

 

 

  1. Végezd el :
    101 – ( 52 : 4 - 7 ) . 8 =
    1999 – 63 : 9 + 6 · 12 =
    ( 127 · 48 – 6 · 16 ) : 10 =
  2. Hány olyan természetes szám van, amely 7 ezresből, 2-nél nem több százasból, 9 tízesből és 8 egyesből áll? Sorold fel és add össze őket!
  3. Tölts ki minden üresen hagyott téglalapot olyan pozitív egész számmal,amely az alatta levő, vele érintkező téglalapokban levő számok szorzata!


  4. A 18–at többféle módon fel lehet bontani 3 pozitív egész szám szorzatára. Írd le az összes lehetőséget! Vigyázz, a tényezők felcserélésével nem kapsz különböző megoldásokat!
  5. Hányat kell lépnie Picurnak, hogy eljusson Szundihoz, aki 12 m + 71 dm + 70 cm távolságra lakik tőle ? Picur egy lépésének hossza 60 cm .
  6. Az ábrán levő azonos betűk azonos értékűek .Három A hány B-t ér ?

    A+ B + B = X
    A = B + X

    Válaszodat röviden indokold !
  7. Hányféleképpen tudod kiolvasni TUDOR nevét? Csak jobbra és lefelé léphetsz!

    T U D
    U D O
    D O R

    Írd le a lehetőségeket! pl :
    T U D
           O
           R
  8. Péter 10 Sk–val a zsebében vasárnap este elhatározza , hogy spórolni fog napi fagyijára. Hétfőtől kezdve minden reggel kap anyukájától 1 Sk–t, és minden délután vesz magának 3 Sk–ért fagylaltot. A hét melyik napján eszik utoljára fagylaltot? Vigyázz, ez szöveges feladat, nem elég csak feleletet irni!
  9. Annának és Lacinak van fejenként 33 darab 1 cm hosszúságú pálcikája. Anna a lehető legnagyobb négyzetet, Laci a lehető legnagyobb egyenlő oldalú háromszöget szeretné kirakni. Melyik alakzatnak lesz nagyobb a kerülete és mennyivel? A pálcikákat nem szabad eltörni .
  10. A kocka lapjait 1- től 6-ig megszámoztuk. Négy azonos számozású kockából raktuk ki ezt a építményt.



    Milyen szám nem állhat az 1 –essel szemközti lapon? Mi áll?
    Milyen szám nem állhat a 3 –assal szemközti lapon? Mi áll?

 

 

  1. Számítsd ki: (80 - 20) . 4 =
    (21 + 4) . 3 + 25 =
    80 - 20 . 4 =
    21 + 4 . 3 + 25 =
    107 - (68 : 4 - 10) =
    2000 + 21 . 4 - 252 : 3 =
  2. Egy üres láda tömege 2 kg, a benne levő gyümölcsé 20 kg. Az autó 18 teli ládát hozott. A targonca 350 kg-ot bír el. Elbírja egyszerre az összes ládát? 
  3. Döntsd el, hogy a négyzetnek az 1/4-e, 1/3-a, 1/2-e vagy más törtel kifejezhető része van-e besötétítve! Hányad rész maradt fehéren?

    a)                         b)  
  4. Az ábrán látható alakzat gyufaszálakból van kirakva. Jelöld be azt a két gyufaszálat, amelyeket ha elvesszük, akkor a megmaradt gyufaszálak négy négyzetet alkotnak!


  5. Juli 14 kockából 11 kocka hosszúságú, 3 bástyás falat épített. Milyen hosszú falat építhet 42 kockából?


  6. Egy hordóban a vízoszlop a hordó magasságának 3/5-éig ér. Rajzold le! Még négy vödörrel öntöttek bele, így a hordó megtelt. Hány vödör víz fér a hordóba?
  7. Az ábrán látható lapot először az 1., majd a 2. szaggatott vonal mentén összehajtjuk úgy, hogy mindig az 1 maradjon a legalsó szám. Milyen sorrendben helyezkednek el egymás fölött a hajtogatás után a számok?
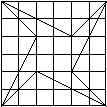
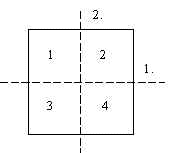
    wpe19.jpg (3205 bytes)
  8. Egy 4 cm méretű fakockát pirosra festünk, majd 1 cm élű kisebb kockákra daraboljuk fel. Hány kis kocka keletkezik? Hány olyan kis kocka lesz, amelynek egyik oldala sem piros? Hány kis kockának lesz 3 oldala piros?

 

 

1. Végezd el:                758 + 36 . 2 – 189 : 3 =

                                     215 . 68 – 215 . 58 =

                                    ( 102 . 8 – 560 : 10 ) . 100 =

                                    222 – 22 . ( 12 . 4 – 160 : 4 ) : 2 =

  

2. Mely számokra gondoltam? Az eredményt ide jegyezd le!

            a, Mennyi a 3078 százas nagyságrendre kerekített értéke?          .................................

            b, Mennyi a 3500 felének a négyszerese ?                                  .................................

            c, Hány cm a 12 m + 12 dm + 12 cm ?                                     .................................

            d, Hány méter a 10 km egyötöde ?                                            .................................

 3. Milyen számjegyek kerülhetnek a     , illetve a ▼ helyére ?            6 8    8             6 ▼ 4 8

a) Ha a két szám egyenlő ?                                                       = ...............       = ...............

b) Ha a két szám különbsége a lehető legnagyobb                        = ...............       = ...............

c) Ha az első szám 370 – nel nagyobb                                        = ...............       = ............... 

 

4. Keress  összefüggést a számok között, és írd be a hiányzókat!

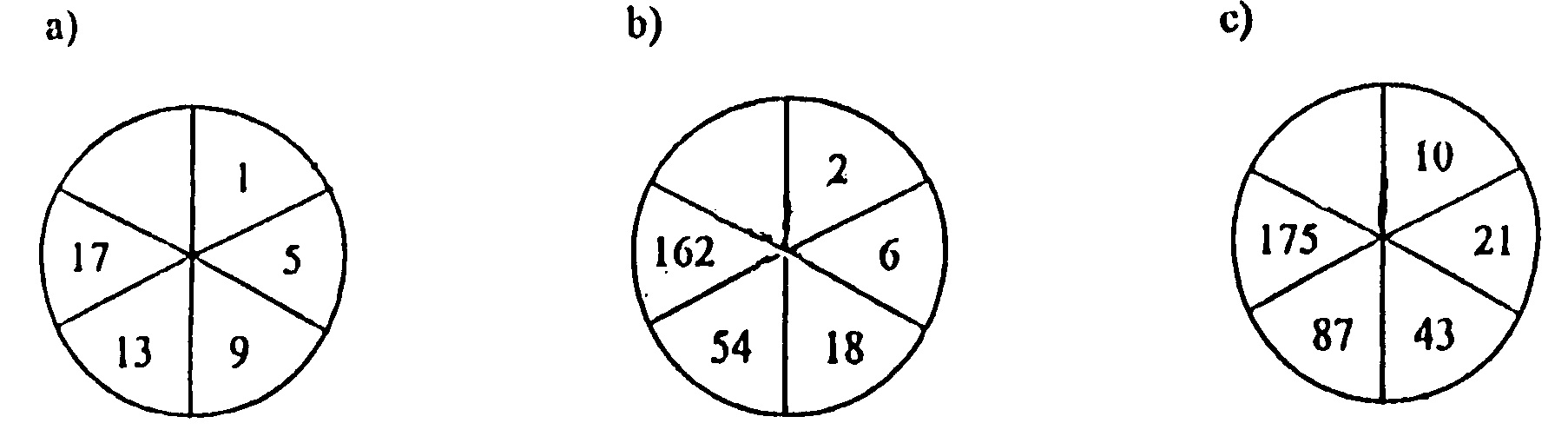
5. A kisegér és a kis elefánt kör alakú pályán versenyt futnak. Hat kört kell lefutniuk. Az indulás 10 óra 30 perckor van. A kis elefánt 6 perc alatt, a kis egér 4 perc alatt fut le egy    kört.   

 

 a)      Melyikük lesz a győztes ? 

b)      Írd le, hogy az indulástól számítva hányadik percben lesz a START – vonalban a kis elefánt: 0 perc, 6, perc,.................................................................................................... .........................................................................................................................................

c)      A kis elefánt célbaérkezésének időpontja: ...........................óra ..............................perc

6. Levente hétfőn 3 barátjának mondott el egy találós kérdést. A három barát kedden külön-külön öt ismerősének mondta tovább. Tudjuk, hogy a három barátnak nincs közös ismerőse. Hányan ismerték a találós kérdést szerdán ?

 

7. Az út mentén 4 tanuló áll névsor szerint: Anna, Béla, Cili és Dani. Anna és Béla között 97 méter, Anna és Dani között 207 m a távolság. Cili Bélától és Danitól egyforma távolságra áll. Milyen messze van Anna Cilitől ? Rajzolj, számolj, ellenőrizz!

8. Három gyufásdobozt különbözőféleképpen rakhatunk egymásra. Milyen különböző magassága lehet az ilyen három gyufásdobozból álló építménynek, ha a gyufásdoboz hosszúsága 5 cm, szélessége 3 cm és magassága 1 cm ? Sorold fel!9. Hét korongot az ábra szerint helyeztünk az asztalra. A korongok között három zöld színű van és a többi fehér. Rajzold le, hogy helyezkedhetnek el az asztalon a zöld színű korongok! Nem tekintjük különbözőnek azt az elrendezést, amikor forgatással átvihető egyik helyzetéből a másikba. Keress többféle elrendezést! Színezd be a zöld korongokat!
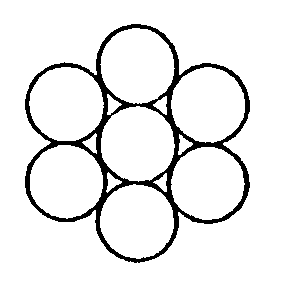
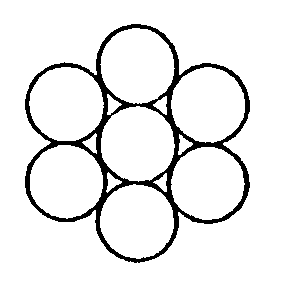
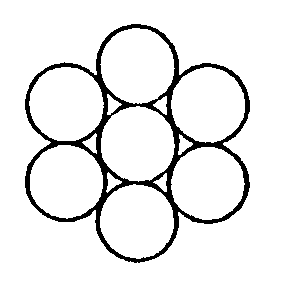
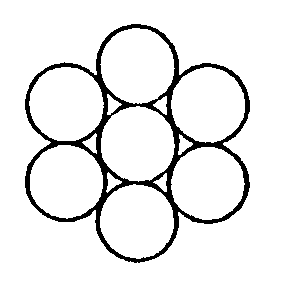
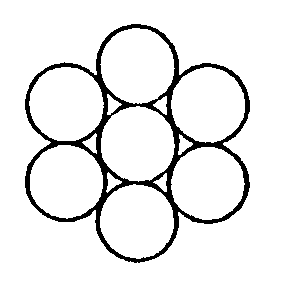
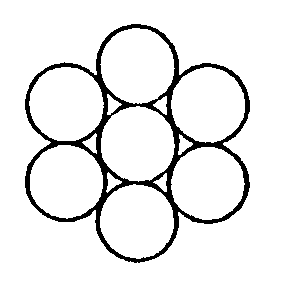