4 osztályos    

matematika

magyar szlovák

 

    
8 osztályos    

matematika

magyar

szlovák

 

  1. Adjuk össze a kifejezéseket, és győződjünk meg a rendezés helyességéről az r = 1 behelyettesítéssel!
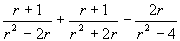
  2. Az emberi testben a vér mennyisége megközelítőleg a testsúly 7.6%-a. Eszerint hány kg vére van egy 75 kg súlyú felnőttnek?
  3. Oldjuk meg a valós számok halmazán az egyenletet, és végezzük el a próbát.
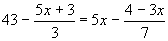
  4. A munkás 1550 Kčs fizetést kapott 100-as és 50-es bankjegyekben. Összesen 21 bankjegyet kapott. Melyikből mennyit kapott?
  5. Szerkesszük meg az ABCD egyenlő szárú trapézt, ha d(AB) = 8,4 cm, v = 3,5 cm és az ABC szög 90°!
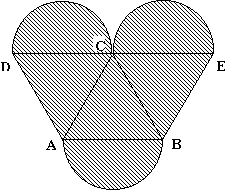
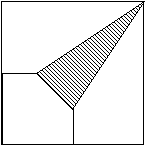
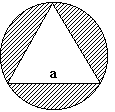
  6. Számítsuk ki az ábrán látható satírozott alakzat területét, és kerületét, ha az ABC háromszög egyenlő oldalú, és d(AB) = 20 cm, amely egyúttal a kör átmérője is. Az EC és CD szakaszok is körök átmérői.
  7. Gyufából az alábbi ábrasorozatot raktuk ki:

    Ha folytatjuk a sorozatot, hány szál gyufa kell a 10. ábra kirakásához?

 

  1. Egyszerűsítsétek az kifejezést és győződjetek meg az eredmény helyességéről a = 2 esetére!
  2. Ha a négyzet oldalát 28%-kal növeljük, a kerülete 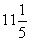m-rel nő. Számítsátok ki az eredeti négyzet oldalát!
  3. Oldjátok meg a valós számok halmazán és végezzétek el a próbát
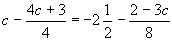
  4. Az apa háromszor olyan idős, mint a fia. Tizenkét évvel ezelőtt az apa kilencszer volt idősebb a fiánál. Hány éves az apa, és hány a fia?
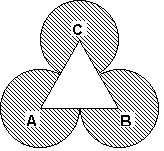
  5. Számítsátok ki az ábrán látható satírozott alakzat területét és kerületét, ha az ABC háromszög egyenlő oldalú és d(AB)=6 cm.
  6. Szerkesszétek megaz ABC -et, ha b=6 cm, ta=5 cm és tb=6 cm.
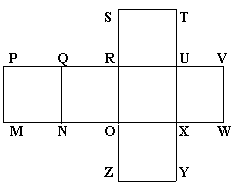
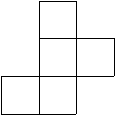
  7. Az ábra egy élei mentén felvágott és kiterített papírkockát ábrázol. Ha ezt ismét kockává hajtogatjuk, akkor melyik csúcsok találkoznak P-vel, Q-val, M-el?

 

  1. Oldd meg az egyenletet, és végezd el a próbát!
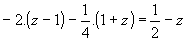
  2. Egy bögre térfogata 5/8 liter. Hány bögre vízzel lehet megtölteni egy ötliteres üveget?
  3. Két toll és három ceruza 25 koronába kerül. Három toll és két ceruza ára 25,50 korona. Melyik drágább: a toll, vagy a ceruza? Mennyivel?
  4. Egy vállalat termékeinek 7/12 -ed részét külföldön értékesítette, a maradék 2/5 -ét itthon adta el. Termékeinek hány százaléka van még raktáron?
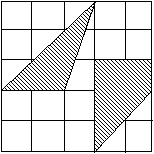
  5. Az ábrán látható négy síkidom közül melyiknek a területe a legnagyobb? Mekkora ?
  6. Egy 20 méteres hatósugarú szórófejes öntözöt az út szélétöl 16 méterre állítottak fel. Öntözés után az út szélének milyen hosszú része lesz vizes?
  7. Hol kell megépíteni az út mentén az autóbuszmegállót hogy az ábrán megjelölt A és B településektöl egyenlö távolságra legyen? Szerkeszd meg a megálló helyét!
                             A +



                                                                 + B

            út   ________________________________   
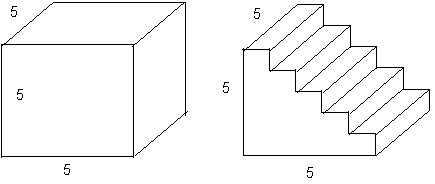
  1. Melyik test felszíne nagyobb? Mennyivel?
  2. Péternek négyzet alakú egyforma nagyságú kártyái vannak. Egy nagy négyzetet rakott ki belölük, de 5 kártyája kimaradt. Amikor egy kártyával többet tett egy sorba, a nagy négyzet kirakásához hiányzott 8 kártyája. Hány kártyája volt?
  3. Egy 120 centiméter hosszú rúdból 5 egyforma részt vágtak le. Milyen hosszúak a levágott részek, ha hosszuk egész centiméter, és a maradék nem volt hosszabb 6 cm-nél? Határozd meg az összes megoldást!

 

  1. Végezd el az alábbi műveleteket! (Ne alakítsd tizedestörté)
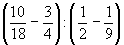
  2. Oldd meg a következő egyenletet! Eredményed ellenőrizd!
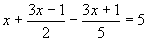
  3. Péter most kétszer olyan idős, mint Pál. Négy évvel ezelőtt viszont Péter háromszor olyan idős volt mint Pál. Hány évesek most.
  4. Egy egyenlőszárú háromszög alapja 24 cm, szára 13 cm hosszú. Számítsd kia háromszög területét!
  5. Egy téglalap oldalai a=40 cm, ill. b=20 cm. Az a oldal hosszát 10%-kal, a b oldal hosszát 20%-kal csökkentjük. Mennyivel csökken a téglalap területe?
  6. Szerkeszd meg a az ABC háromszöget, ha c=5 cm, a B csúcsnál lévő szög nagysága 60°, illetve a háromszög köré írt kör sugara 3 cm.
  7. A nagy félkör átmérőjére rajzolt kis félkörök átmérője 1 cm. Mekkora a vonalkázott rész területe?
  8. Öt egész szám szorzata 1. Mennyi lehet az összegük legkisebb értéke?
  9. Az alakzat területe 15 cm2. Határozzátkok meg a kerületét!

 

  1. Oldd meg a következő egyemletet és eredményed ellenőrizd!
  2. Végezd el az alábbi müveleteket!
  3. Egy szövettekercsnek eladták a 2/3 részét, és még 7 métert. Így a negyedénél 4 méterrel rövidebb maradt. Hány méter szövet volt a tekercsben eredetileg?
  4. Két szám összege 35. Ha az elsö számot 20 %-kal növeljük és a másodikat 20 %-kal csökkentjük akkor az összegük 3-mal növekszik. Határozd meg ezeket a számokat!
  5. Egy egyenlö szárú derékszögü háromszög területe 98 cm2. Mekkorák a háromszög oldalai, kerülete és a köré írt kör sugara?
  6. Szerkessz háromszöget ha a = 4cm, b = 4cm és tc = 3,5cm!
  7. Az 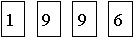számkártyákból hány olyan négyjegyü szám rakható ki, amelyben a 9-esek nem állnak egymás mellett!
  8. A körbe írt négyzet területe hányadrésze a kör területének?
  9. Az elsö száz természetes szám között hány olyam szám van, amely sem kettövel, sem hárommal nem osztható?
  10. A vonalkázott rész hányad része a négyzet területének? (Az oldalakon felezöpontokat vettünk fel, a belsö pont pedig a négyzet szimmetriaközéppontja)

 

  1. a) Egészítsétek ki: (2x + ?)2 = ? + ? + 36 !
    b) Számítsátok ki:
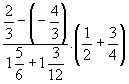
  2. Oldjátok meg a valós számok halmazán 
  3. Egy kötélnek levágták a 2/3 részét, és még 7 métert. Így a negyedénél 4 méterrel rövidebb maradt. Milyen hosszú volt a kötél?
  4. Adott az e egyenes, rajta T pont és a g egyenesen kívül egy A pont. Az A pont az e egyenestől 4 cm, a T ponttól 5 cm távolságra van. Szerkezd meg az A ponton áthaladó, az e egyenest a T pontban érintő kört!
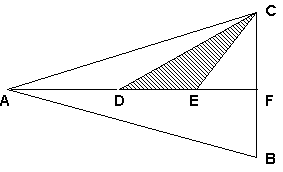
  5. Hányadrésze a bevonalkázott terület a háromszög területének, ha az F pont a BC szakasz felezőpontja, D és E az AF szakasz harmadolópontjai?
  6. Az ábrán látható körbe írt szabályos háromszög oldalhossza a = 2Ö,3 cm. Számítsd ki a satírozott alakzat területét!
  7. Panninak hat nyári ruhája van. Nyaraláshoz csomagol. Hányféleképpen állíthatja össze a ruhatárát, ha 5 ruhát visz magával?

 

  1. Határozzátok meg mikor van az alábbi kifejezésnek értelme, egyszerüsítsétek és végezzétek el a próbát az x = -1 értékre:
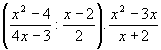
  2. A vállalat dolgozói három részlegen dolgoznak. Az elsőn 30-an, ami az összes dolgozó 15%-a. A másodikon az összes munkás 10%-a dolgozik. Hányan dolgoznak az egyes részlegeken?
  3. Alakítsátok szorzattá a következő kifejezéseket:
    4(x – z) + (z – x) =
    a2 + 2ab + b2 – ac – bc =
    (x – y) 2 – 4 =
  4. Oldjátok meg a valós számok halmazán a következő egyenletet, és végezzétek el a próbát:
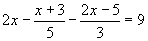
  5. Szerkesszétek meg azt az ABC háromszöget melyben c = 8 cm, tc = 5 cm és vc = 3 cm.
  6. Adott az 5 cm oldalhosszúságú négyzet. Határozzátok meg a bevonalkázott alakzatok területét.
  7. Hányszor kell a legnagyobb egyjegyű számhoz hozzáadni a legnagyobb kétjegyű számot, hogy megkapjuk a legnagyobb háromjegyű számot?

 

  1. a) Egészítsétek ki 


    b) Alakítsátok szorzattá
  2. Oldd meg a következő egyenletet a valós számok halmazán és végezd el a próbát:
  3. Egy tört nevezője 5-tel nagyobb mint számlálója. Ha a számlálóját 15-tel, nevezőjét pedig 3-mal nagyobbítjuk, olyan törtet kapunk amely egyenlő az eredeti tört reciprokával. Melyik ez a tört?
  4. Szerkesszétek meg azt az ABC háromszöget melyben a = 4,5 cm va = 3 cm r = 4 cm. (köré írt kör sugara)
  5. A benzin árát 10%-kal emelték majd 10%-kal csökkentették, így 30 fillérrel kevesebbe került mint eredetileg. Mennyibe került eredetileg?
  6. Számítsátok ki az egyenlő oldalú háromszögbe és a háromszög köré írt körök által meghatározott körgyűrű területét, ha a háromszög oldala a = 12 cm!
  7. Az ábrán egy kocka hálóját látjuk. A kocka mindegyik csúcsánál kiszámoljuk az adott csúcsot tartalmazó három lapon álló számok szorzatát. Mekkora a szorzatok közül a legnagyobb és a legkisebb?
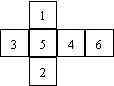
  8. A 86?? számban egészítsétek ki a kérdőjelek helyét úgy, hogy az így kapott négyjegyű szám egyidejűleg osztható legyen hárommal, néggyel és öttel.

 

  1. Végezd el a kijelölt műveleteket!

  1. Oldd meg a következő egyenletet, végezd el a próbát!

  1. Alakítsd szorzattá!

 

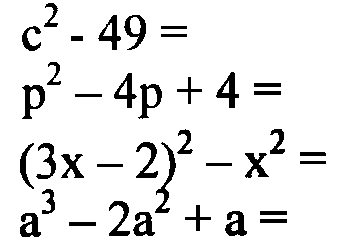
  1. Fejezd ki az x-et:

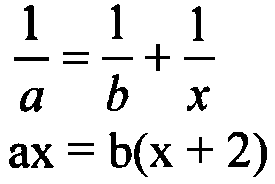
  1. Melyik az a természetes szám, amelynek 12-szerese 20-szal nagyobb,mint a nála 2-vel kisebb szám 14-szerese?
  2. Oldjátok meg a prím számok halmazán:

  1. Szerkesszétek meg az ABCD trapézt,ha  ½AB½ =8 cm;  ½ACB½  =90,  ½ABC½  =60, ½AD½ =4cm
  2. Egy háromszög oldalainak az aránya 3:4:5 a kerülete pedig 24 cm.Mekkorák a háromszög oldalai? Határozzátok meg a háromszög és a köré írt kör területét!
  3. Hány olyan n egész szám van , amelyre 6/(n-3)tört értéke egész szám?
  4. Egy téglalap oldalai a = 40 cm és b = 10 cm.Az a oldal hosszát 30%-kal , a b oldal hosszát 10%-kal csökkentjük. Hány százalékkal csökken a téglalap területe?

 

 

1.        Egyszerűsítsd a kifejezést, majd állapítsd meg, hogy mikor van a kifejezésnek értelme!

         

     2. Oldd meg az egyenletrendszert, és végezd el a próbát!     

        

3.      A kirándulás , melynek egy főre eső költsége 160 Sk volt, 7,5 %-kal drágult. Az osztály 396 Sk-val fizetett többet. Hány tanuló ment kirándulni?

 

4.       A forgáshenger magassága megegyezik az alaplap átmérőjével. A henger felszíne 471cm2. Határozzátok meg a henger térfogatát.( Legyen p = 3,14)

 

5.       Szerkesszétek meg az ABC háromszöget, ha ½AB½ =70 mm ; a c oldalhoz tartozó magasság: vc = 50 mm; az a oldalhoz tartozó súlyvonal: ta = 55 mm.

 

6.        A 13 cm és 15 cm sugarú körök egymást az A és B pontokban metszik úgy, hogy a körök középpontjai az AB egyenes által meghatározott ellentett félsíkokban vannak. Számítsátok ki a körök O1, O2 középpontjainak távolságát és az O1AO2B négyszög területét, ha az AB húr hossza 24 cm.

 

7. Az e, f, g, h egyenesek egymást az A, B, C, D, E, F pontokban metszik. Számítsátok ki az     ABCD négyszög belső szögeinek a nagyságát!                                             

 

1.        A 2002 egy olyan négyjegyű pozitív egész szám, amelyben a számjegyek összege 4. Hány ilyen négyjegyű pozitív egész szám van?